"The entropic principle
In Ref. [3], a novel proxy for observers was proposed: the production of matter entropy. The formation of any complex structure (and thus, of observers in particular), is necessarily accompanied by an increase in the entropy of the environment. Thus, entropy production is a necessary condition for the existence of observers. In a region where no entropy is produced, no observers can form. The "entropic principle" is the assumption that the number of observers is proportional, on average, to the amount of entropy produced:
In Ref. [3], a novel proxy for observers was proposed: the production of matter entropy. The formation of any complex structure (and thus, of observers in particular), is necessarily accompanied by an increase in the entropy of the environment. Thus, entropy production is a necessary condition for the existence of observers. In a region where no entropy is produced, no observers can form. The "entropic principle" is the assumption that the number of observers is proportional, on average, to the amount of entropy produced:
nobs ∝ ∆S . (1.1)"
Taken from: Bousso et al.
Now I have to connect Entropy with PATH.
Bousso is giving us a way to navigate the String Theory Landscape of solutions. As he writes in the quote I posted in the first note of this series. "String theory produces an eternally inflating multiverse". Also we can say that there are 10500 solutions. We need new methods to search such huge sets. Notice that the exponent is a "regular" number, i.e., the kind of number we are used to deal with in daily life. Say, five hundred cents make five bucks. As an exponent though, it goes beyond what we are used to consider. In The Sand Reckoner, Archimedes treats his contemporaries to such big numbers.
""But I will try to show you by means of geometrical proofs, which you will be able to follow, that, of the numbers named by me and given in the work which I sent to Zeuxippus, some exceed not only the number of the mass of sand equal in magnitude to the Earth filled up in the way described, but also that of the mass equal in magnitude to the universe." [4]"
Archimedes invented exponents and found the rules to treat them. That is the mathematical key to deal with big numbers.
Now enter computer science and Entropy. The PATH variable, and S.
You can do a simple experiment to get an idea of what I am talking about. Type John in Google.
You get:
Results 1 - 10 of about 1,060,000,000 for john [definition]. (0.44 seconds)
There are 109 successes found in half a second! Archimedes would be overjoyed.
Obviously Page and Brin brought math to the masses. I am sure that somewhere in their PhD theses, they must use the ideas represented by the PATH variable. Boltzmann gave us the same insight with:
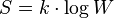 .
.
Now I have to connect Entropy with PATH.
Bousso is giving us a way to navigate the String Theory Landscape of solutions. As he writes in the quote I posted in the first note of this series. "String theory produces an eternally inflating multiverse". Also we can say that there are 10500 solutions. We need new methods to search such huge sets. Notice that the exponent is a "regular" number, i.e., the kind of number we are used to deal with in daily life. Say, five hundred cents make five bucks. As an exponent though, it goes beyond what we are used to consider. In The Sand Reckoner, Archimedes treats his contemporaries to such big numbers.
""But I will try to show you by means of geometrical proofs, which you will be able to follow, that, of the numbers named by me and given in the work which I sent to Zeuxippus, some exceed not only the number of the mass of sand equal in magnitude to the Earth filled up in the way described, but also that of the mass equal in magnitude to the universe." [4]"
Archimedes invented exponents and found the rules to treat them. That is the mathematical key to deal with big numbers.
Now enter computer science and Entropy. The PATH variable, and S.
You can do a simple experiment to get an idea of what I am talking about. Type John in Google.
You get:
Results 1 - 10 of about 1,060,000,000 for john [definition]. (0.44 seconds)
There are 109 successes found in half a second! Archimedes would be overjoyed.
Obviously Page and Brin brought math to the masses. I am sure that somewhere in their PhD theses, they must use the ideas represented by the PATH variable. Boltzmann gave us the same insight with:
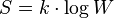 .
.There we have our friend log, the inverse of the exponential function.
Bousso then, is telling us to concentrate on the exponent, not the number. Follow the exponent, not the number. His Entropic principle draws attention to exponents. The number of observers he says, is proportional to the amount of Entropy produced, formula (1.1).
My only point here is that the PATH variable in UNIX limits the size of the landscape. I guess that expert Unix programmers, have long definitions for their PATH variable, not like the default one I put in the previous note.
Software engineers then keep track of long searches with this elementary method, and more sophisticated ones like version control, or trace software. Here you have an example.
More to come.
Bousso then, is telling us to concentrate on the exponent, not the number. Follow the exponent, not the number. His Entropic principle draws attention to exponents. The number of observers he says, is proportional to the amount of Entropy produced, formula (1.1).
My only point here is that the PATH variable in UNIX limits the size of the landscape. I guess that expert Unix programmers, have long definitions for their PATH variable, not like the default one I put in the previous note.
Software engineers then keep track of long searches with this elementary method, and more sophisticated ones like version control, or trace software. Here you have an example.
More to come.



No comments:
Post a Comment